Research Blog: Diving Deep into the Mamba Model Implementation
Introduction
The Mamba model, introduced in the paper Mamba: Linear-Time Sequence Modeling with Selective State Spaces by Albert Gu and Tri Dao, represents a significant advancement in sequence modeling. Unlike traditional transformer-based architectures that scale quadratically with sequence length, Mamba achieves linear-time complexity using selective state space models (SSMs). This blog post explores the technical depth of implementing Mamba in PyTorch, as provided in the given model.py and scan.py files, breaking down the architecture, key components, and challenges encountered in the implementation.
Background: State Space Models and Mamba
State Space Models (SSMs) provide a framework for modeling sequences by representing them as a system of differential equations. Traditionally, SSMs like S4 (Structured State Space Sequence Models) use fixed parameters, limiting their adaptability to input data. Mamba introduces selective SSMs, where parameters like ( \Delta ), ( B ), and ( C ) are input-dependent, enabling the model to adapt dynamically to the sequence context. This selectivity, combined with a linear-time scanning mechanism, makes Mamba both efficient and expressive for long-sequence modeling tasks.
The implementation provided is a minimal, single-file PyTorch version of Mamba, designed for clarity and ease of understanding. It includes the core components of the model, such as the Mamba block, selective scan, and RMS normalization, while also supporting pretrained model loading from HuggingFace.
Key Components of the Implementation
1. Model Configuration with ModelArgs
The ModelArgs dataclass defines the hyperparameters for the Mamba model, such as:
d_model: The hidden dimension of the model.n_layer: The number of Mamba layers.vocab_size: The size of the vocabulary for the embedding layer.d_state: The latent state dimension (( N ) in the Mamba paper).expand: The expansion factor to compute the inner dimension (( d_{\text{inner}} = d_{\text{model}} \times \text{expand} )).dt_rank: The rank of the input-dependent step size (( \Delta )), with an "auto" option to set it as ( \lceil d_{\text{model}} / 16 \rceil ).d_conv: The kernel size for the 1D convolution.scan_mode: The mode for the selective scan algorithm (cumsumorlogcumsumexp).
The __post_init__ method ensures that d_inner and dt_rank are computed appropriately and that vocab_size is padded to a multiple of pad_vocab_size_multiple for efficient processing.
2. Mamba Model Architecture
The Mamba class encapsulates the full model, consisting of:
- Embedding Layer: An
nn.Embeddinglayer maps input tokens to dense vectors of sized_model. - Residual Blocks: A stack of
n_layerResidualBlockmodules, each containing a normalization layer and aMambaBlock. - Normalization: An
RMSNormlayer applied before the final output projection. - Language Model Head: A linear layer (
lm_head) that projects the hidden states back to the vocabulary size, with tied weights to the embedding layer for efficiency (as described in the "Weight Tying" paper).
The forward method processes input token IDs through the embedding layer, applies the residual blocks, normalizes the output, and projects it to logits over the vocabulary.
3. ResidualBlock
The ResidualBlock wraps a MambaBlock with a normalization layer (RMSNorm) and a residual connection. The forward pass follows the structure:
[ \text{output} = \text{MambaBlock}(\text{RMSNorm}(x)) + x ]
This differs from the official Mamba implementation, which uses a fused Add-Norm-Mamba structure for performance. The provided implementation prioritizes simplicity and numerical equivalence, applying normalization before the Mamba block and adding the residual connection afterward.
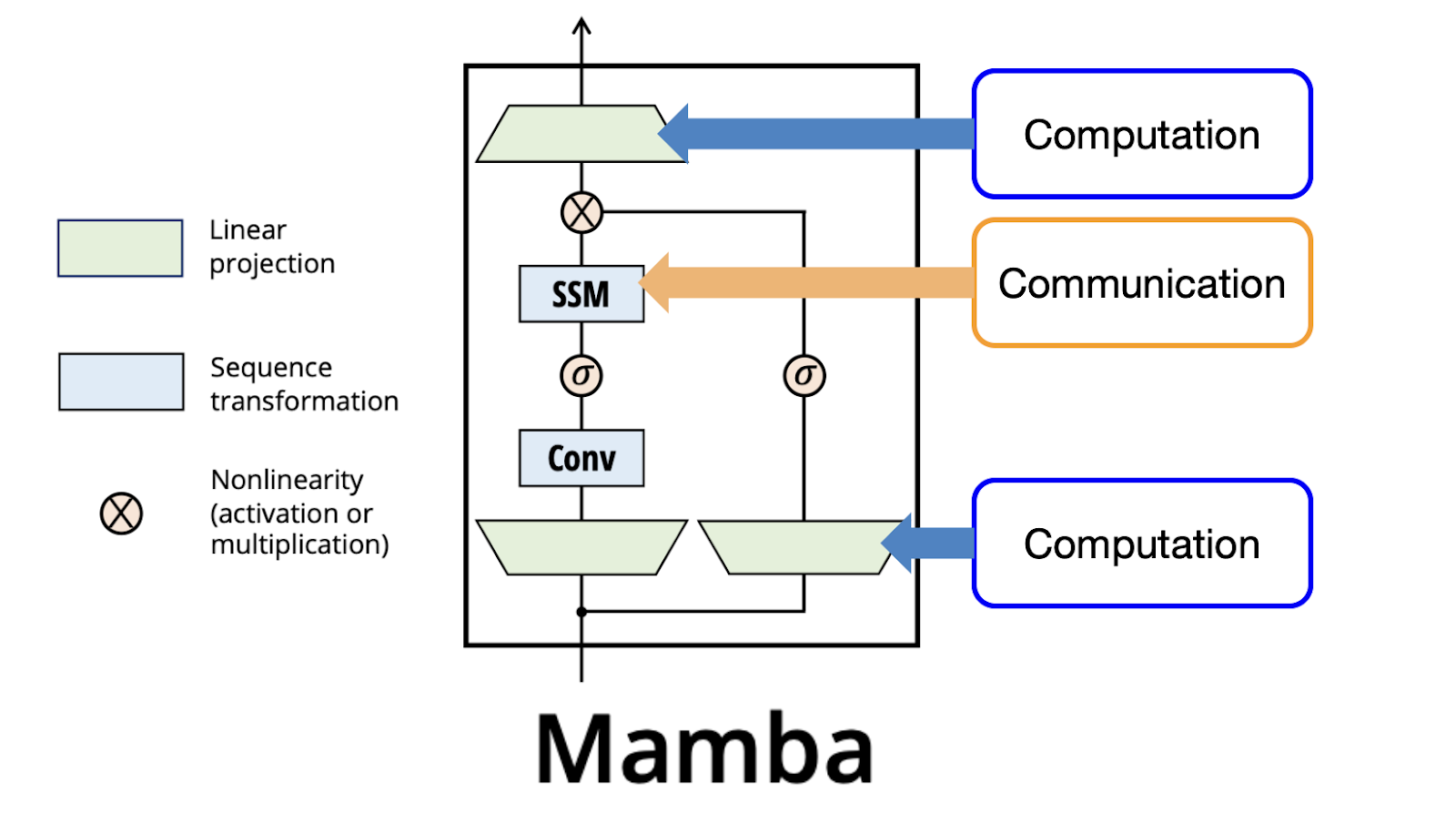
4. MambaBlock
The MambaBlock is the core of the model, implementing the selective SSM as described in Figure 3 of the Mamba paper. Its components include:
- Input Projection: A linear layer (
in_proj) projects the input fromd_modelto2 * d_inner, splitting the output intoxand a residual (res). - 1D Convolution: A grouped 1D convolution (
conv1d) with kernel sized_convprocesses the input sequence, introducing local context. - SSM Parameters:
- The
x_projlinear layer generates input-dependent parameters ( \Delta ), ( B ), and ( C ). - The
dt_projlayer projects ( \Delta ) fromdt_ranktod_inner. - ( A ) is parameterized as
A_log(logarithm of the state transition matrix) to ensure stability, and ( D ) is a learnable vector.
- The
- Selective Scan: The
ssmmethod computes the state space dynamics using theselective_scanfunction. - Output Projection: A linear layer (
out_proj) maps the SSM output back tod_model.
The forward pass applies the convolution, SiLU activation, the selective SSM, and a gated residual connection before the final projection.
5. Selective Scan (scan.py)
The selective_scan function implements Algorithm 2 from the Mamba paper, computing the SSM output given input ( u ), step size ( \Delta ), and parameters ( A ), ( B ), ( C ), and ( D ). It supports two modes:
- Cumsum Mode: Uses cumulative summation to compute the SSM recurrence. This is straightforward but can suffer from numerical instability for long sequences.
- Logcumsumexp Mode: A more numerically stable "Heisen sequence" approach, using complex logarithms to compute the recurrence in log space, reducing overflow risks.
The provided scan.py includes a test script that compares the two modes, showing that the mismatch between them grows with sequence length due to numerical precision differences.
6. RMSNorm
The RMSNorm class implements Root Mean Square Normalization, a variant of layer normalization that scales the input by the inverse of its root mean square value. It is used in both the ResidualBlock and the final normalization step of the Mamba model.
7. Pretrained Model Loading
The from_pretrained method in the Mamba class enables loading pretrained weights from HuggingFace models (e.g., state-spaces/mamba-2.8b). It loads the model configuration and state dictionary, mapping weights to the corresponding model parameters while handling differences in naming conventions (e.g., removing the backbone. prefix).
Challenges and Considerations
Implementing Mamba in PyTorch involves several challenges:
- Numerical Stability: The selective scan algorithm requires careful handling to avoid numerical overflow, especially for long sequences. The
logcumsumexpmode addresses this by operating in log space, but it introduces additional complexity. - Selective Parameters: Unlike traditional SSMs, Mamba's input-dependent ( \Delta ), ( B ), and ( C ) require careful tensor manipulation to align dimensions and ensure efficient computation.
- Convolution Padding: The 1D convolution uses padding to maintain sequence length, requiring precise configuration to avoid information loss.
- Pretrained Weight Compatibility: Loading pretrained weights involves mapping between the official implementation's state dictionary and the custom implementation, handling potential mismatches in parameter names or shapes.
Insights from the Implementation
- Modularity: The code is structured for clarity, with separate classes for
Mamba,ResidualBlock,MambaBlock, andRMSNorm. This makes it easier to understand and extend compared to a monolithic implementation. - Flexibility: The
scan_modeparameter allows switching betweencumsumandlogcumsumexp, enabling experimentation with numerical stability trade-offs. - Efficiency: Weight tying and grouped convolutions reduce memory usage and computational cost, making the implementation suitable for resource-constrained environments.
- Extensibility: The
from_pretrainedmethod facilitates integration with pretrained models, allowing researchers to leverage existing weights for fine-tuning or evaluation.
Potential Improvements
- Performance Optimization: Fusing the Add-Norm-Mamba structure, as done in the official implementation, could improve runtime performance.
- Parallel Scan: The current selective scan is sequential, but parallel implementations (e.g., using associative scan techniques) could further reduce latency.
- Additional Features: Supporting bidirectional processing or integrating attention mechanisms could enhance the model's capabilities for specific tasks.
- Robustness Testing: Extending the test script in
scan.pyto cover edge cases (e.g., very long sequences or extreme values) would ensure robustness.
Conclusion
The provided Mamba implementation is a concise yet powerful demonstration of selective state space modeling in PyTorch. By breaking down the architecture into modular components and addressing numerical stability, it offers a clear entry point for researchers and practitioners interested in exploring linear-time sequence models. The ability to load pretrained weights further enhances its utility, making it a valuable tool for advancing research in efficient sequence modeling.
For further reading, refer to:
- Mamba paper: arXiv:2312.00752
- The Annotated S4: srush.github.io/annotated-s4